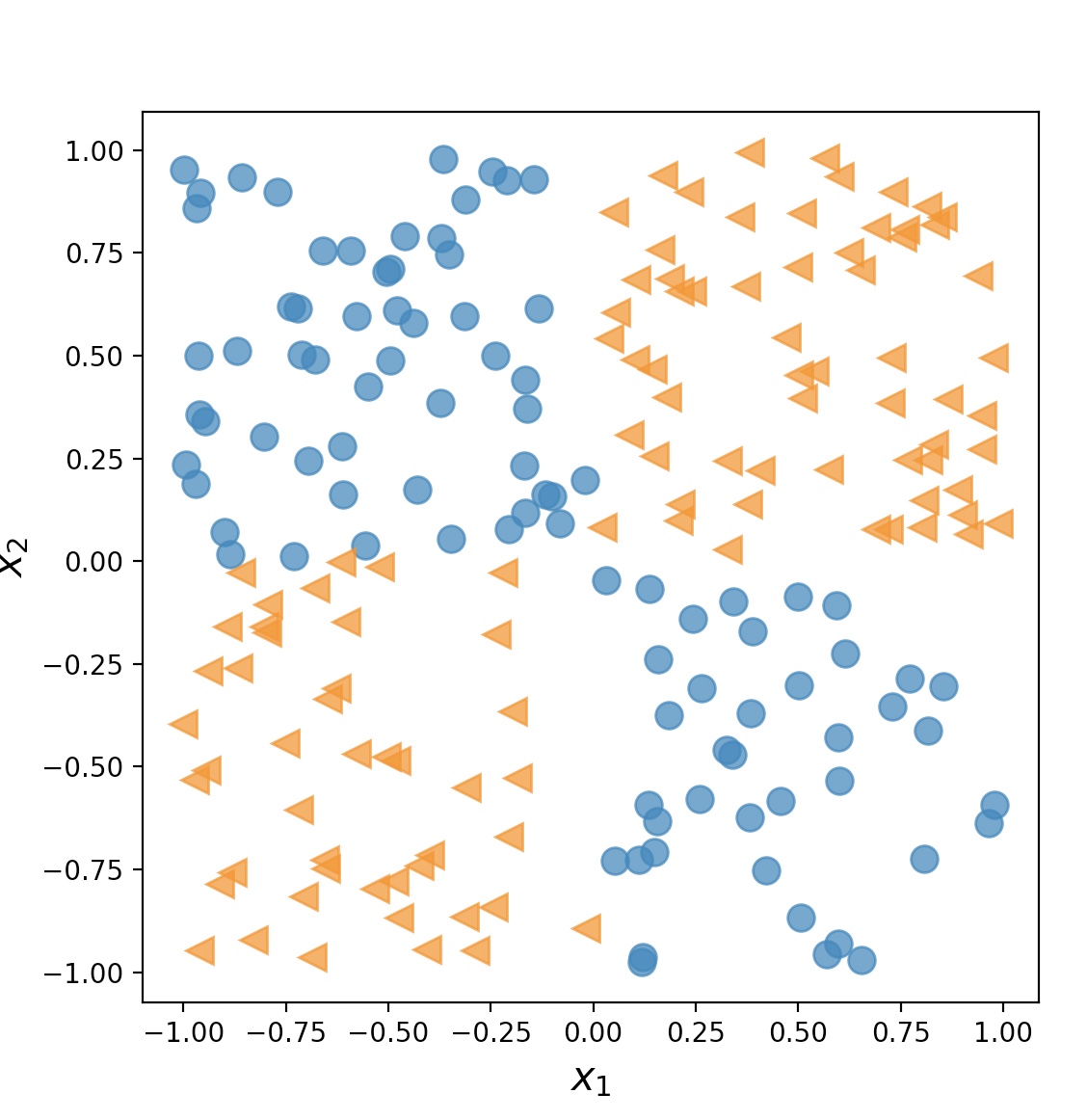
XOR 분류 문제는 두 개의 클래스 사이에서 비선형 결정 경계를 감지하는 모델의 수용 능력을 분석하기 위한 전통적인 문제이다.
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
tf.random.set_seed(1)
np.random.seed(1)
x=np.random.uniform(low=-1, high=1, size=(200, 2))
y=np.ones(len(x))
y[x[:, 0]*x[:, 1]<0]=0
x_train=x[:100, :]
y_train=y[:100]
x_valid=x[100:, :]
y_valid=y[100:]
fig=plt.figure(figsize=(6, 6))
plt.plot(x[y==0, 0], x[y==0, 1], 'o', alpha=0.75, markersize=10)
plt.plot(x[y==1, 0], x[y==1, 1], '<', alpha=0.75, markersize=10)
plt.xlabel(r'$x_1$', size=15)
plt.ylabel(r'$x_2$', size=15)
plt.show()
일반적으로 층이 많을 수록, 층에 뉴런 개수가 많을 수록 모델의 수용 능력이 높다.많은 파라미터를 가지고 있으면, 모델이 복잡한 함수를 근사할 수 있지만, 모델이 클 수록 훈련하기 힘들다.
또한 과대적합 되기도 쉽다.
은닉층이 없는 간단한 모델
model=tf.keras.Sequential()
model.add(tf.keras.layers.Dense(units=1,
input_shape=(2, ),
activation='sigmoid'))
model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_6 (Dense) (None, 1) 3
=================================================================
Total params: 3
Trainable params: 3
Non-trainable params: 0
_________________________________________________________________
model.compile(
optimizer=tf.keras.optimizers.SGD(),
loss=tf.keras.losses.BinaryCrossentropy(),
metrics=[tf.keras.metrics.BinaryAccuracy()])
hist=model.fit(x_train, y_train, validation_data=(x_valid, y_valid),
epochs=200, batch_size=2, verbose=0)
fit 메서드로 훈련 후 반환된 값으로 시각화MLxtend 라이브러리를 사용하여 검증 데이터와 결정 경계를 시각화
$pip3 install mlxtend
from mlxtend.plotting import plot_decision_regions
import matplotlib.pyplot as plt
history=hist.history
fig=plt.figure(figsize=(16, 4))
ax=fig.add_subplot(1, 3, 1)
plt.plot(history['loss'], lw=4)
plt.plot(history['val_loss'], lw=4)
plt.legend(['Train loss', 'Validation loss'], fontsize=15)
ax.set_xlabel('Epochs', size=15)
ax=fig.add_subplot(1, 3, 2)
plt.plot(history['binary_accuracy'], lw=4)
plt.plot(history['val_binary_accuracy'], lw=4)
plt.legend(['Train Acc.', 'Validation Acc.'], fontsize=15)
ax.set_xlabel('Epochs', size=15)
ax=fig.add_subplot(1, 3, 3)
plot_decision_regions(X=x_valid, y=y_valid.astype(np.integer), clf=model)
ax.set_xlabel(r'$x_1$', size=15)
ax.xaxis.set_label_coords(1, -0.025)
ax.set_ylabel(r'$x_2$', size=15)
ax.yaxis.set_label_coords(-0.025, 1)
plt.show()
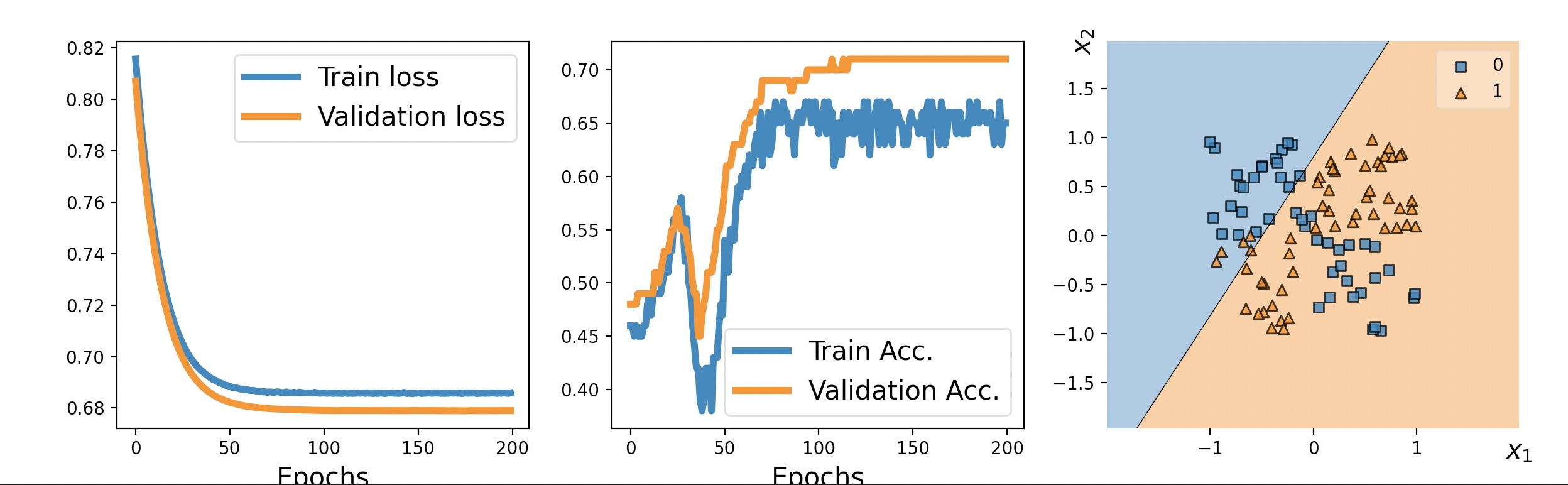
위처럼 은닉층이 없는 간단한 모델은 선형 결정 경계만 찾을 수 있다.(XOR 풀 수가 없다)
따라서 훈련 데이터셋과 검증 데이터셋의 손실이 매우 높고, 분류 정확도가 매우 낮다.
비선형 결정 경계를 찾기 위해서 비선형 활성화 함수를 사용한 한 개 이상의 은닉층을 추가할 수 있다.
일반 근사 이론(universal approximation theorem)에 의하면, 하나의 은닉층과 매우 많은 은닉 유닛을 가진
피드포워드 신경망은 임의의 연속 함수를 비교적 잘 근사 시킨다.
네트워크에서 은닉층의 개수는 네트워크의 폭을 은닉 유닛의 개수는 네트워크의 깊이를 깊게 한다고 한다.
네트워크의 너비(폭) 대신 깊이가 깊어지면, 비슷한 모델 수용 능력을 달성하는데 필요한 파라미터 개수가 적다는 장점이 있다.
하지만 넓은 폭의 모델에 비해 깊은 모델은 그레이디언트가 폭주하거나, 소멸될 수 있어 훈련하기 어렵다
은닉 층 추가
tf.random.set_seed(1)
model=tf.keras.Sequential()
model.add(tf.keras.layers.Dense(units=4, input_shape=(2, ), activation='relu'))
model.add(tf.keras.layers.Dense(units=4, activation='relu'))
model.add(tf.keras.layers.Dense(units=4, activation='relu'))
model.add(tf.keras.layers.Dense(units=1, activation='sigmoid'))
model.summary()
Model: "sequential_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_5 (Dense) (None, 4) 12
_________________________________________________________________
dense_6 (Dense) (None, 4) 20
_________________________________________________________________
dense_7 (Dense) (None, 4) 20
_________________________________________________________________
dense_8 (Dense) (None, 1) 5
=================================================================
Total params: 57
Trainable params: 57
Non-trainable params: 0
_________________________________________________________________
model.compile(
optimizer=tf.keras.optimizers.SGD(),
loss=tf.keras.losses.BinaryCrossentropy(),
metrics=[tf.keras.metrics.BinaryAccuracy()])
hist=model.fit(x_train, y_train, validation_data=(x_valid, y_valid), epochs=200, batch_size=2, verbose=0)
여러개의 은닉층을 가진 모델의 비선형 경계
from mlxtend.plotting import plot_decision_regions
import matplotlib.pyplot as plt
history=hist.history
fig=plt.figure(figsize=(16, 4))
ax=fig.add_subplot(1, 3, 1)
plt.plot(history['loss'], lw=4)
plt.plot(history['val_loss'], lw=4)
plt.legend(['Train loss', 'Validation loss'], fontsize=15)
ax.set_xlabel('Epochs', size=15)
ax=fig.add_subplot(1, 3, 2)
plt.plot(history['binary_accuracy'], lw=4)
plt.plot(history['val_binary_accuracy'], lw=4)
plt.legend(['Train Acc.', 'Validation Acc.'], fontsize=15)
ax.set_xlabel('Epochs', size=15)
ax=fig.add_subplot(1, 3, 3)
plot_decision_regions(X=x_valid, y=y_valid.astype(np.integer), clf=model)
ax.set_xlabel(r'$x_1$', size=15)
ax.xaxis.set_label_coords(1, -0.025)
ax.set_ylabel(r'$x_2$', size=15)
ax.yaxis.set_label_coords(-0.025, 1)
plt.show()

위의 모델은 데이터에서 비선형 경계를 찾았으며, 훈련 데이터셋에서 100% 정확도를 달성했다.
검증 데이터셋의 정확도는 95%로 모델이 약간 과대적합되어 있다고 해석할 수 있다.